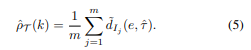research_augmentation_EEG/Augmentation methods.md

Manifool

https://arxiv.org/abs/1711.09115 This method was used in article Data Augmentation with manifold exploring, which is relevant to eeg research. Geometric robustness of deep networks: analysis and improvement The manifool paper discusses creation of an algorithm to measure geometric invariance of deep networks. Then discusses how to make the networks better at managing those transformations. Authors try to search for minimal fooling transformation to measure the invariance of a NN. Then they do fine tuning on transformed examples. First preliminaries. Lets say we have a set of transformations \Tau. Then small \Tau is a transformation which belongs to \Tau. Now how to measure how the effect of transformation, respectivelly we are looking for a metric which would quantitatively measure how much does transformation change sample. Lets look at some metrics applicable for this problem:

• Measure l² distance between transformation matrices. This doesn't reflect the semantics of transformations such as rotation vs translation.
• Squared L² distance, difference between two transformed images. . This is better since it is dependent on sample. Tho not good enough.
• Length of the shortest curve between two transformations, geodesic distance. This metric is the one used in manifool algorithm.

As you can see the metric is between two transformations. The first transformation is always identity transformation, we will call it e. Manifool in particular tries to find minimal transformation, with minimal distance from e, which leads to misclassification. Then the invariance score of classifier is calculateg as an average minimal fooling transformation.

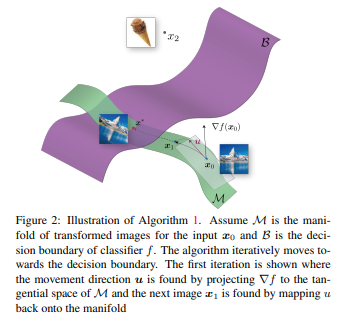
Manifool algorithm Algorithm to find minimal fooling transformation. The main idea is to iteratively move from image towards decision boundary of the classifier, while staying on the transformation manifold. Each iteration is composed of two steps:

• Choosing the movement direction
• Mapping the movement onto manifold

This iteratively continues until hitting classification boundary of classifier.
Choosing movement direction and length. Lets imagine binary classifier k(x) = sign(f(x)), where f: Rⁿ -> R is an arbitrary differentiable classification function. In paper for simplicity authors consider x for which label is 1. Therefore assuming f(x) > 0, for this example. Then to reach decision boundary in shortest way we need to choose direction which maximaly reduces f(x) therefore moving against derivation of f in x, opposite of gradient. Then some serious math is involved, I need more time to fully grasp it.

Experiments In the experiments, the invariance score for minimal transformations, defined in (5), is calculated by finding fooling transformation examples using ManiFool for a set of images, and computing the average of the geodesic distance of these examples. On the other hand, to calculate the invariance against random transformations, we generate a number of random transformations with a given geodesic distance r for each image in a set and calculate the misclassification rate2 of the network for the transformed images.

My summary We can take pretrained model. Then make dataset tailored to that dataset which will contain minimal fooling samples. That dataset will be used to fine tune.

Data Augmentation with Manifold Exploring Geometric Transformations for Increased Performance and Robustness

https://arxiv.org/pdf/1901.04420 Authors did create dataset with images lying on decision boundary to maximize variance to which network is exposed to during training. Models used were: ResNet, VGG16, InceptionV3. Comparing

• no augmentation
• random augmentation - rotational and horizontal flipping
• manifool
• Random erasing - replaces random patches of image with gaussian noise

GAN architecture was used to generate synthetic images. Not exactly an EEG paper, but methods can be used for BCI I thinnk